Trigonométrie : ce qu’il faut retenir en 3e
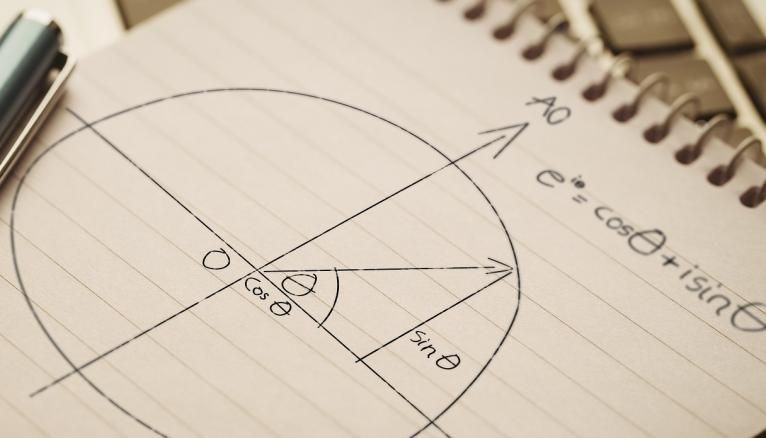
La trigonométrie est un concept mathématique qui fait le lien entre les mesures des angles des triangles rectangles et les longueurs de leurs côtés. Ne prenez pas la tangente, on vous explique simplement ce qu’il faut savoir en classe de 3e.
Comment comprendre simplement la trigonométrie ?
La trigonométrie est un sous-domaine des mathématiques, qui consiste à étudier les rapports entre les mesures des angles et les mesures des longueurs dans un triangle rectangle. L’analyse de ces rapports permet de déduire des distances qu’on ne peut mesurer, par exemple, quand le triangle rectangle est très grand.
La trigonométrie sert donc de base dans de nombreux domaines, tels que la construction, mais aussi l’astronomie et l’optique, deux domaines dans lesquels on utilise des triangles « virtuels » pour calculer des distances.
À quoi sert la trigonométrie ?
La trigonométrie s’applique aux triangles rectangles. Les formules trigonométriques permettent de :
Déduire la longueur de deux côtés lorsqu’on connaît la longueur d’un côté et la mesure d’un angle.
Calculer la mesure des angles lorsqu’on connaît la longueur de deux côtés.
La trigonométrie est ainsi le premier outil utilisé par les astronomes depuis l’Antiquité. Les formules trigonométriques permettent de mesurer la distance entre deux étoiles selon l'angle qu'elles forment entre elles.
D’autres domaines de la vie courante font appel aux règles de trigonométrie. C’est le cas de la navigation, de la cartographie, de la construction : tous les domaines dans lesquels il faut estimer des rapports de distances en ne disposant pas de l’ensemble des données.
Il existe même des applications très surprenantes de la trigonométrie. Par exemple, les fonctions Sinus et Cosinus permettent de décrire les sons produits par les instruments de musique. La trigonométrie est donc une base pour étudier la musique et l’harmonie des sons ! Plus généralement, les fonctions de trigonométrie servent pour décrire la propagation de toutes sortes d'ondes. C'est pourquoi leur étude est fondamentale pour comprendre le monde qui nous entoure.
Comment tracer un cercle trigonométrique ?
Pour utiliser les fonctions Sinus et Cosinus, savoir tracer un cercle trigonométrique est un passage obligé.
Voici les étapes préparatoires pour dessiner votre cercle :
1. Sur un papier, tracez deux lignes perpendiculaires.
2. Nommez ces deux axes, respectivement des abscisses (« x ») et des ordonnées (« y »).
3. À l’aide d’un compas, tracez le cercle en prenant l’intersection des deux axes comme point central.
Vous avez la base de votre cercle trigonométrique. Il faut ensuite placer les angles.
4. Divisez le cercle en quatre parts égales, puis en huit parts égales et en six parts égales, puis de nouveau en douze parts égales. À chaque fois, les angles sont mesurés par un radian : lorsque l’angle représente un quart de la circonférence et vaut donc : 2π/4 = π/2 radians.
5. Pour chaque angle, il faut donc noter la mesure correspondante exprimée en radian.
Une fois que vous avez placé les angles, utilisez les formules des relations trigonométriques pour disposer les coordonnées de l’ensemble des angles.
Pour calculer les coordonnées x et y de n'importe quel point sur le cercle, il faut utiliser la formule : x = x0 + r * cos(theta) et y = y0 + r * sin(theta). Dans celle-ci, theta est l'angle en radians formé entre l'abscisse positive et le point sur le cercle.
Comment repérer les trois côtés d’un triangle ?
Il existe trois côtés dans un triangle rectangle :
L'hypoténuse est le plus long côté du triangle : il est situé en face de l’angle droit.
Le côté opposé est celui qui est en face de l’un des angles aigus du triangle.
Le côté adjacent est celui qui est à côté de l’un des angles aigus du triangle, mais n’est pas l'hypoténuse.
On ne parle d’un côté adjacent ou opposé qu’en relation avec l'un des angles aigus du triangle.
Quelles sont les six fonctions de base de la trigonométrie ?
Il existe six fonctions de base dans la trigonométrie :
Le sinus (sin) ;
le cosinus (cos) ;
la tangente (tan) ;
la sécante (sec) ;
la cosécante (csc) ;
la cotangente (cot).
Les plus connues sont le sinus, le cosinus et la tangente.
Quelles sont les relations entre les fonctions de trigonométrie ?
Toutes les fonctions de trigonométrie entretiennent un lien entre elles qu’il est possible de représenter visuellement dans le cercle trigonométrique. Par exemple, le cosinus est le rapport entre le côté adjacent à l'angle par rapport à l'hypoténuse. Le sinus est le rapport entre le côté opposé à l'angle par rapport à l'hypoténuse. Quant à la tangente, elle est le rapport entre la fonction sinus et cosinus.
Quelles sont les formules de trigonométrie à retenir en 3e ?
Le sinus, le cosinus et la tangente sont les trois fonctions de trigonométrie que vous devez retenir. Voici leurs formules mathématiques.
Comment calculer un sinus et un cosinus?
Le sinus se calcule en divisant le côté opposé par l'hypoténuse.Soit, pour un triangle rectangle ABC :
Sin (A) = BC/AB
Le cosinus se calcule en divisant le côté adjacent par l'hypoténuse.Soit pour le même triangle rectangle ABC :
Cos (A) =AC/AB
Comment calculer la tangente ?
La tangente se calcule en divisant le côté opposé par le côté adjacent. Soit, pour un triangle ABC :
Tan (A) = BC/AC
Quels moyens mnémotechniques utiliser en trigonométrie ?
Pour retenir les trois principales fonctions trigonométriques, vous pouvez mémoriser « soh cah toa » pour sinus = opposé sur hypoténuse (soh), cosinus = adjacent sur hypoténuse (cah)et tangente = opposé sur adjacent (toa).
Si vous appliquez nos astuces, vous saurez choisir la formule à utiliser pour calculer le côté adjacent, le côté opposé ou l'hypoténuse. L’univers de la trigonométrie vous plaît ? Découvrez également notre article sur le théorème de Thalès.
Réviser la Trigonométrie : les quiz
Après avoir lu cette fiche récapitulative du cours, vous voilà prêt(e) à tester vos connaissances en trigonométrie ! Découvrez nos quiz de révision sur la thématique de la trigonométrie ⬇️
